Model of Knowledge by Fitzgerald Systems

Considerations in design shall, at minimum, include

Deflections
Deformations
Static Loads
Dynamic Loads

Fundamental to the above consideration is the deduction of stresses (loads applied over a unit surface area) versus the material strength. If stresses exceed the elastic deformation limit then irreversible plastic deformation will start potentially leading to the eventual catastrophic failure of the material.

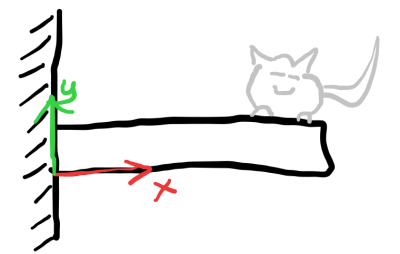
Let's consider a critter of known mass is standing on a fixed beam at a known distance from the beam origin and you want to know at which point in the beam are the stresses highest.

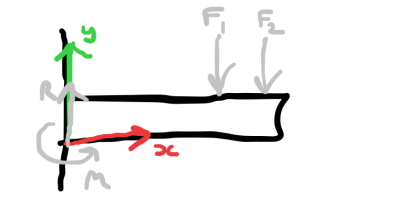
This can be abstracted as follows and, with Newton's third law, it is possible to determine reaction forces and moments.

Let's determine the forces and moments on the beam on an arbitrary distance from the beam origin. To so we make examine the forces and moments at x that keep the beam in equilibrium. This force is parallel with the beam's cross section is called Shear and V is its symbol. But how are Moment at x related to Shear at x?

Click here to see how the below formula is derived

For a body in equilibrium we know $ \Sigma F = 0 $ and $ \Sigma M = 0 $ Taking a positive force in direction of axis and a positive moment follows the Right Hand about axis.

Therefore $ R = F_1 + F_2 $ and $ M = F_1 . x_1 + F_2 . x_2 $

If the moment at distance x is $ M_x $ then $ M_x = M - R.x $ then $ M_x + \delta M = M - R(x + \delta x) $

This rearranges to $ \delta M = M - R.x - R. \delta x - M_x $

Which simplifies to $ \delta M = -R. \delta x $

Which rearranges to $ R = - {{dM} \over {dx}} $ but as the force acting on the cross section is opposite to the reaction force at the origin of the beam then we can generalize that $ V = {{dM} \over {dx}} $

$ V = {{dM} \over {dx}} $ or Shear is equal to the rate of change of Moment along a beam.

Model of Knowledge by Fitzgerald Systems

User Tools

Site Tools

Page Tools